| Reply to Thread New Thread |
|
|
#1 |
|
|
An ESPN Outside the Lines statistical survey has found what they say to be evidence that the US Open draw has not been random over the last 10 years. They stated that there would be a 1 in 300,000 probability that this would happen if the draw was random. Naturally, US Open chairman Brian Earley and other US Open representatives denied that anything was wrong with the draw process.
Full article and video |
|
|
|
|
#2 |
|
|
|
|
|
|
|
#4 |
|
|
|
|
|
|
|
#5 |
|
|
But here's what I don't get... If someone was fixing the draw, why wouldn't they fix it in a manner that wasn't quite so skewed toward skewering young Americans in the process? Or perhaps I think that's the case because those are the only players they cite. But there are other options. Other scrubs from other countries that would be pretty sure bet victims and no one would miss?
Or maybe that's what they did regularly and they worked in some Americans from time to time as evidence it wasn't... But that fact alone (the number of young Americans screwed in the process) would support the idea that, if something fishy is going on, it's not anyone at the USTA/USA tennis establishment. It just seems strange. And sometimes, randomness is bizarrely random. I don't know. I'd need more than this. |
|
|
|
|
#6 |
|
|
It seems to me they need a larger sampling than ten US Opens, even if it is a little unusual it happened for both the men's and women's draws. The world of random numbers is weird and sometimes looks not so random. Just like flipping a coin 100 times will give a random streak of heads or tails and it will look not very random at all. In this experiment, try to replace only 4 of the higher numbers (lets say remove rank 127 player and replace with say 55 and do it for number 1 seed for 4 years), in that case you will see that US Open results will be very similar to that of other tournaments. It really doesn't take much for couple fluke draws to make such a big effect. Another thing to point at.. in an interview with Andrew Swift where he makes a comparison that the chance of draw happening that way was 1 in about 300,000. Same as flipping heads 18 times in a row on first flip... ok but flipping same coin with these results HTHTHTHTHTHTHTHTHT or HHTTHHTTHHTTHHTTHH or any other single possible combination will ALSO give you 1 in about 262,144 chance ((1/2)^18) So, his analogy is really bad, imo |
|
|
|
|
#7 |
|
|
But here's what I don't get... If someone was fixing the draw, why wouldn't they fix it in a manner that wasn't quite so skewed toward skewering young Americans in the process? Or perhaps I think that's the case because those are the only players they cite. But there are other options. Other scrubs from other countries that would be pretty sure bet victims and no one would miss? |
|
|
|
|
#10 |
|
|
I don't get the numbers they present about halfway down the page. They're showing the percentage of their simulations that were "at least as easy" as the average of the real draws. So the ideal number should be 50%. Half the simulations are easier, half are harder. Instead the AO and FO women's draws are almost 100%. That means nearly every one of the thousand simulations gave harder draws than the real ones. This is just as unlikely as the 0% USO draws. I think they're done something really wrong in their analysis.
|
|
|
|
|
#11 |
|
|
I don't get the numbers they present about halfway down the page. They're showing the percentage of their simulations that were "at least as easy" as the average of the real draws. So the ideal number should be 50%. Half the simulations are easier, half are harder. Instead the AO and FO women's draws are almost 100%. That means nearly every one of the thousand simulations gave harder draws than the real ones. This is just as unlikely as the 0% USO draws. I think they're done something really wrong in their analysis. By the way, just because there were only 10 US Opens in the study doesn't really make a difference because the goal was to find how likely it would be for those 10 US Opens to have the kind of draws they did, not for any one of the tournaments to have an easy draw. If it was just one year, it would be much easier for the tournament directors to cast it off as an anomaly, but 10 years is more difficult. |
|
|
|
|
#12 |
|
|
|
|
|
|
|
#14 |
|
|
Alright, so it does look like the results are skewed. They are using the metric of the world ranking of the player who gets drawn as seed 1 or 2 first round opponent.
I think it became this way due to the fact that USO has had draws of significantly lower ranked players than only the 33-128 that the simulations include. Naturally, when you have an outlier like the 518-ranked player (  ) the average is now going to be heavily skewed downward. To the degree that the running average simply cannot be reflected properly by a simulation that only goes to 128. ) the average is now going to be heavily skewed downward. To the degree that the running average simply cannot be reflected properly by a simulation that only goes to 128.This is my guess. I think it would be borne out if we can look at the average world rank of the unseeded players in the draw for each tournament. If this is the case, I'd expect that we would find that the average rank of players in the draw for the USO would be lower than the rest, followed by Wimbledon, then French and Australian would have comparively higher average unseeded player ranks. Or, the way to correct for this bias would be to assign a player a rank associated with how their current ranking matches with all of the other players in the draw, thereby assigning the lowest player a rank of 128, and try running this again. The average world ranking metric is inheriently flawed for this analysis. |
|
|
|
|
#16 |
|
|
Alright, so it does look like the results are skewed. They are using the metric of the world ranking of the player who gets drawn as seed 1 or 2 first round opponent. "To get something as far away from 80 as 100 is extremely unlikely," Swift said. "If you looked at the other three Grand Slams over the same time period, the average rank of the opponents of the top two seeds in both the men's and women's sides was close to 80. It was close enough that it wasn't statistically significant." |
|
|
|
|
#17 |
|
|
I could well be wrong, but I think they did do this The statement that you quote I had read as being about the data simulation. An explicit statement about whether or not actual rankings were corrected to match the simulation would really be helpful. |
|
|
|
|
#18 |
|
|
Just seen that they link to a page with more details of their analysis
How 'Outside the Lines' analyzed the U.S. Open tennis tournament draw ESPN analyzed the men's and women's draws in each of the four Grand Slam tennis tournaments: the Australian Open, French Open, Wimbledon and U.S. Open. The analysis, which was done by analytics specialist Alok Pattani of the ESPN Stats & Information Group, focused on the top two seeds in each tournament. It began with the compilation of the men's draws for all Grand Slams since the 2001 Wimbledon -- 41 total tournaments (11 Wimbledons and 10 each for the Australian, French, and U.S. Opens.) The study used the ATP rankings information from immediately before every Grand Slam draw for each men's player in a Grand Slam (since 2001). Those rankings, along with the placements for the 32 seeded players, were used to re-rank the players 1-128 -- the total number of players in a Grand Slam tournament. So if a player was ranked 575th in the ATP rankings and that was the second-worst ranking among all players in the draw, he was re-ranked 127th. This re-ranking was used to examine the strength of the opponents facing the top two seeds. An opponent ranking closer to the minimum rank of 33 meant the top two seeds drew a relatively difficult opponent, while a ranking close to the maximum of 128 would be representative of a relatively easy first-round draw. The same data-gathering procedure was used for the women's draws, using the corresponding predraw WTA rankings. Table A (below) shows the U.S. Open men's top two seeds' first-round opponents the past 10 years and those opponents' ranks among all players in the tournament. Table B (below) shows the U.S. Open women's top two seeds' first-round opponents the past 10 years and those opponents' ranks among all players in the tournament. Turning opponent rankings into "draw difficulty" scores To further measure opponent difficulty, ESPN assigned scores to a player's draw by using the opponent's rank compared to all possible opponent ranks that the player could have faced in that round. So if a top two seed faced the 33rd-ranked player in the first round, he/she would get a difficulty score of 0.995 for that round; if he/she faced the 128th-ranked player in the first round, the score for that round would be 0.005. An average opponent (ranked around 80th or 81st), would correspond to a difficulty score near 0.500, which should be the average difficulty score over several years of draws. Once ESPN had the first-round draw difficulty scores for each of the top two seeds, the scores were averaged by Grand Slams across the 10-year span (11 years for Wimbledon) to see if the top two seeds got relatively easy or difficult draws at each individual Grand Slam. The findings in the first round of the U.S. Open stood out. Simulating thousands of random draws It is always the case that fluctuations among tournaments and draws could be attributed to random chance -- by design, the draws have an element of randomness built into them. However, tests can be designed to see if the results produced by these random draws actually appear to be truly random. For example, the 0.326 and 0.313 first-round average scores for the top two men's and women's seeds at the U.S. Open seem quite low compared to the expected average of .500, but how often would scores that low over a 10-year span actually occur by random chance? Because ESPN knew the actual format of these draws, one way to answer these types of questions was to simulate the draws themselves many times and see how often results as extreme as those found in the data occurred. So ESPN created a "fake" draw sheet, with players ranked 1-128 getting placed into slots according to the way a Grand Slam bracket works. Repeating this procedure 10 times (11 for Wimbledon) generated a set of draws comparable to what was found in the draws from actual tournaments. Then ESPN looked at the first-round opponents for the top two seeds from the simulated draws and calculated their draw difficulty scores across the same time span as with the actual draws. This exercise was repeated 1,000 times, providing a simulated distribution of 1,000 average draw difficulty scores for the top two seeds over 10 years (11 for Wimbledon). Because the simulated distribution came from draws randomized the same way that tennis' governing officials told ESPN they randomly constructed draws for the Grand Slams, it was used to benchmark what was found with the actual draws and to determine how likely that was to occur by random chance. Those are ESPN's findings, reported here. To ensure that the methodology was sound, ESPN asked Dr. Andrew Swift, past chairman of the American Statistical Association Section on Statistics in Sport and an assistant mathematics professor at the University of Nebraska at Omaha, to evaluate the data, calculations and work. He said the analysis and its methodology were sound, and he used the same methodology to run calculations -- with up to 1 million repetitions -- and got nearly identical results. "Any way you want to look at these, there is significant evidence here that these did not come from a random draw," he said. A note about sample size An initial look at the data and methodology led some USTA officials to question the study's sample size. But sample size is properly accounted for in this analysis because the 10-year average from the actual U.S. Open draws was compared to 1,000 simulated 10-year averages, each created using the same draw procedure, making this an "apples-to-apples" comparison. From this simulated distribution of 10-year averages, ESPN was able to conclude that the margin of the discrepancy of the actual average rankings from what would be expected over a 10-year sample is outside that which would be reasonable by random chance. The 10-year period was selected because the seeding of 32 players in the Grand Slams started at the 2001 Wimbledon tournament, and there have been exactly 10 U.S. Opens since. Said Dr. Swift: "Their argument that 10 years of data is not a big enough sample size is invalid." TABLE A: MEN'S U.S. OPEN DRAWS The first-round opponents for the top two men's seeds at the U.S. Open for the past 10 years, with opponent rank in tournament. 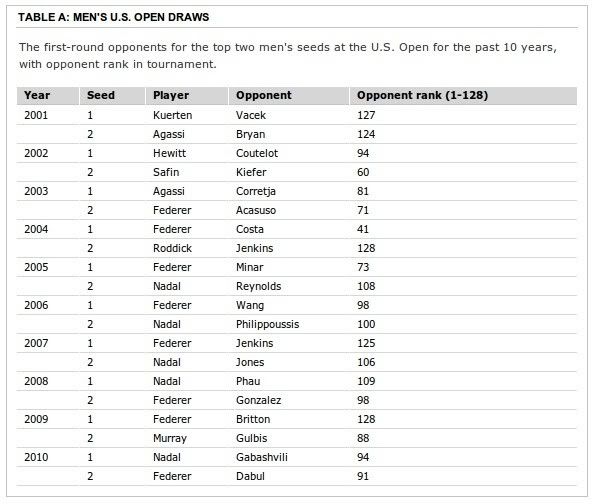 TABLE B: WOMEN'S U.S. OPEN DRAWS The first-round opponents for the top two women's seeds at the U.S. Open for the past 10 years, with opponent rank in tournament. 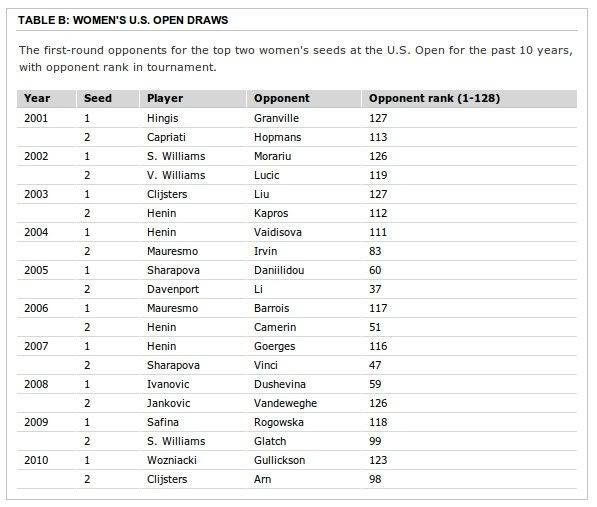 http://espn.go.com/espn/otl/story/_/...ournament-draw |
|
|
|
|
#20 |
|
|
|
|
|
| Reply to Thread New Thread |
«
Previous Thread
|
Next Thread
»
| Currently Active Users Viewing This Thread: 5 (0 members and 5 guests) | |
|
|





 Linear Mode
Linear Mode


