| General Discussion Undecided where to post - do it here. |
| Reply to Thread New Thread |
|
|
#1 |
|
|
|
|
|
|
|
#2 |
|
|
Can you Complete the Square?
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the form |
|
|
|
|
#3 |
|
|
|
|
|
|
|
#4 |
|
|
|
|
|
|
|
#5 |
|
|
|
|
|
|
|
#6 |
|
|
|
|
|
|
|
#7 |
|
|
|
|
|
|
|
#9 |
|
|
Here's what I'm having trouble with:
Quadratic Formula; -b2 +- square root (b2 – 4ac) / 2a -5x2 – 3x – 3=0 I can't get the last part right : A quadratic equation with real or complex coefficients has two solutions, called roots. These two solutions may or may not be distinct, and they may or may not be real. The roots are given by the quadratic formula: In the above formula, the expression underneath the square root sign is called the discriminant of the quadratic equation, and is often represented using an upper case Greek Delta: Quadratic factorization |
|
|
|
|
#10 |
|
|
Given: -5x²-3x-3=0
Using the quadratic equation: -b±√(b²-4ac)/2a → 3±√(9-60)/-10 → 3±√(-51)/-10 You cannot take the square root of a negative value, the only way to express it is using the imaginary value i, where i=√(-1). So you factor in the radical. → 3±√(-1*51)/-10 → 3±√(-1)*√(51)/-10 → 3±√(51)i/-10 Now you can evaluate two separate answers which will have i. Your answer should look like a+bi, where a and b are the real part and i is the imaginary part. |
|
|
|
|
#11 |
|
|
Given: -5x²-3x-3=0 |
|
|
|
|
#12 |
|
|
|
|
|
|
|
#15 |
|
|
|
|
|
|
|
#16 |
|
|
|
|
|
|
|
#18 |
|
|
Given: -5x²-3x-3=0 Here it is: 7x2 – 6x + 3 = 0 6±√(62 – 4 (7) (3)/2(7) 6±√(36-84)/2(7) 6±√(-48)/14 |
|
|
|
|
#19 |
|
|
If the number in the square root is negative it has the imaginary constant i
So just factor the -1 in the square root along with all the factors of 48. =√(-48) =√(48*-1) =√(2*24*-1) =√(2*2*12*-1) =√(2*2*2*6*-1) =√(2*2*2*2*3*-1) You have four factors of 2, one factor of 3, and one factor of -1. When you have two factors of the same number under a radical you can pull that number out, since √(4)=√(2*2)=2. (It's not limited to numbers, if you have two variables that are the same and are being multiplied together you can do the same thing) =2*2√(3*-1) =4√(3)i There's your imaginary part of the equation Having a negative value in the radical is the what the concept of imaginary values are about. You represent the √(-1) as i by factoring the radical. Also, having a positive or negative value in the denominator doesn't change anything about using the quadratic formula except sign changes. |
|
|
|
|
#20 |
|
|
|
|
|
| Reply to Thread New Thread |
«
Previous Thread
|
Next Thread
»
| Currently Active Users Viewing This Thread: 1 (0 members and 1 guests) | |
|
|





 to the form
to the form In this context, "constant" means not depending on x. The expression inside the parenthesis is of the form (x − constant). Thus one converts ax2 + bx + c to
In this context, "constant" means not depending on x. The expression inside the parenthesis is of the form (x − constant). Thus one converts ax2 + bx + c to and one must find h and k.
and one must find h and k.
 where
where  and
and  are solutions.
are solutions. A quadratic equation with real coefficients can have either one or two distinct real roots, or two distinct complex roots. In this case the discriminant determines the number and nature of the roots. There are three cases:
A quadratic equation with real coefficients can have either one or two distinct real roots, or two distinct complex roots. In this case the discriminant determines the number and nature of the roots. There are three cases:
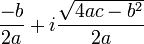 and
and  where i is the
where i is the 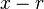 is a factor of the polynomial
is a factor of the polynomial if and only if r is a
if and only if r is a  It follows from the quadratic formula that
It follows from the quadratic formula that In the special case (b2 = 4ac) where the quadratic has only one distinct root (i.e. the discriminant is zero), the quadratic polynomial can be
In the special case (b2 = 4ac) where the quadratic has only one distinct root (i.e. the discriminant is zero), the quadratic polynomial can be 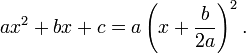
 Linear Mode
Linear Mode


